This chapter introduces two specifically designed zero-inflated beta regression models for analyzing zero-inflated count microbiome data. First we briefly introduce the zero-inflated beta modeling microbiome data (Sect. 13.1). Then we introduce the zero-inflated beta regression (ZIBSeq) and its implementation (Sect. 13.2). Next, we introduce the zero-inflated beta-binomial model (ZIBB) and its implementation (Sect. 13.3). Finally, we briefly summarize the zero-inflated beta regression in microbiome study (Sect. 13.4).
13.1 Zero-Inflated Beta Modeling Microbiome Data
One trend of statistical modeling microbiome data is to use two-part zero-inflated beta regression to detect differential abundance of microbes across clinical conditions or different treatments. The two-part zero-inflated beta regression is attractive because it takes the unique characteristics of microbiome data into account; that is, microbiome data are compositional (quantified by relative abundance), highly skewed, and bounded in [0, 1) and often have many zeros.
A “semi-continuous” or “zero-inflated continuous” data describes a kind of continuous data with a point mass at zero and a right-skewed continuous distribution with a positive values. The raw sequencing reads of microbiome data are absolute abundant counts. However, if the absolute abundant counts are transformed or normalized into relative abundance, then microbiome data can be characterized as a “semi-continuous” or “zero-inflated continuous” data; in which the zero values indicate that either the certain microbes are absent in the sample (structural zeros) or the rare microbes are present but missed due to under-sampling (sampling-zeros), while the continuous distribution of positive values describes the levels of relative abundance among the present microbes (Chai et al. 2018).
Typically, a two-part zero-inflated beta model consists of two sub-models: Part I uses a logistic regression to model the probability of a feature (taxon) having zero values, while Part II uses a beta regression to model the distribution of positive values, i.e., the relative abundance of feature (or taxon) conditionally presented.
So far several two-part beta regression models have been developed for modeling relative abundance of microbiome data, including zero-inflated beta regression (ZIBSeq) (Peng et al. 2016), zero-inflated beta-binomial model (ZIBB) (Hu et al. 2018), zero-inflated beta regression model with random effects (ZIBR) (Chen and Li 2016), and marginalized two-part beta regression (MTPBR) (Chai et al. 2018). Chai et al. (2018) thought that the regression coefficients in Part II in previous two-part zero-inflated beta models is not able to marginally (unconditionally) interpret the covariate effects on the microbial abundance, which is often the interest of microbiome researches. Thus, unlike BESeq and other two-part zero-inflated beta models, MTPBR was proposed to examine covariate effects on the overall marginal (unconditional) mean, while capturing the zero-inflation and skewness of microbiome data (Chai et al. 2018). MTPBR model was derived starting with the conventional two-part model with a beta component in Part II (Chen and Li 2016; Ospina and Ferrari 2012; Peng et al. 2016). Then, in order to obtain the impact of covariates on the overall marginal mean, MTPBR model reparameterizes the likelihood of the conventional two-part model and provides the different interpretation of covariate effects. The distinctive feature of MTPBR is its ability of modeling covariate effects on the marginal mean of the outcome. It was showed that in terms of controlling the type I error, and power as well as robustness, MTPBR has satisfactory performance and outperformed the conventional two-part (CTP) model using the likelihood ratio tests (LRT) for both simulated real data analyses (Chai et al. 2018).
In summary, all the proposed zero-inflated beta models use zero-inflated beta regression to fit relative abundant microbiome data; thus, they aim to take into account the compositional and zero-inflation nature of the microbiome data. However, all these models have their own advantages and limitations.
MTPBR is implemented via SAS NLMIXED procedure, and ZIBR is a longitudinal model that we have introduced in our previous book (2018) (Xia et al. 2018a); thus in this chapter we focus on introducing ZIBSeq and ZIBB.
13.2 Zero-Inflated Beta Regression (ZIBSeq)
ZIBSeq is a zero-inflated beta regression approach for differential abundance analysis of metagenomics data. It is an extension of the generalized linear model (GLM).
13.2.1 Introduction to ZIBseq
ZIBSeq (Peng et al. 2016) was developed to identify differentially abundant features between multiple clinical conditions while addressing the unique characteristics of metagenomics data with small sample size, high dimensionality, sparsity, often with a large number of zeros and skewed distribution under the compositions (proportions) setting. ZIBSeq directly handles the proportion data, assuming that proportional dependent variable can be characterized by the beta distribution.
13.2.1.1 ZIBseq Model
Assume x follows a beta distribution: x~Beta(μ, ϕ), then the density of beta distribution (Ferrari and Cribari-Neto 2004) can be described as a function of u and ϕ:
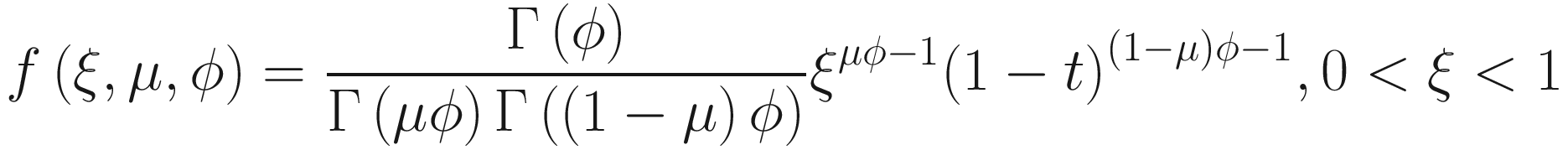
The mean and variance can be parameterized as:
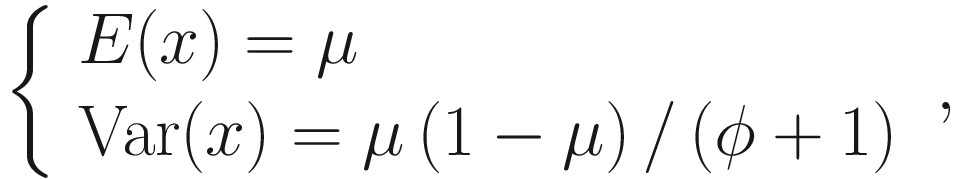
Beta distribution has a wide range of shapes depending on the values of mean and precision parameters. Thus, beta regression models are very suitable to model the continuous response variables of rates and proportions when their values are restricted to the interval (0,1). To model the variable containing zero or one, Ospina and Ferrari in 2012 (Ospina and Ferrari 2012) proposed a more general class of zero-or-one inflated beta regression models for continuous proportions. Given that microbiome data often contains zero instead of one, ZIBSeq was developed based on the zero-inflated beta regression, assuming the response variable has a mixed continuous-discrete distribution with probability mass at zero.
The zero-inflated beta distribution adds a new parameter α to account for the probability of observations at zero. The subsequent mixture density is given as below:
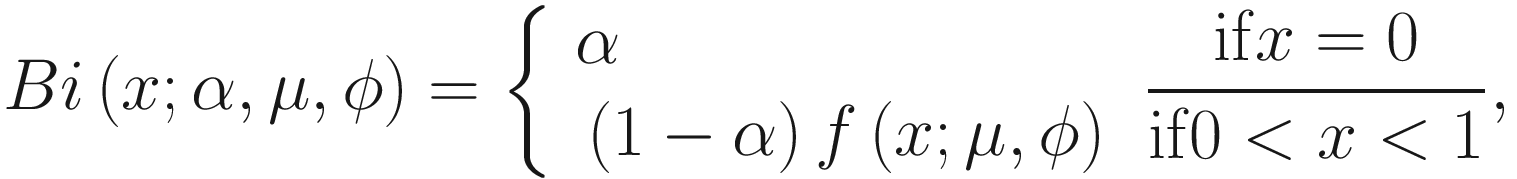
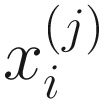 denote the normalized feature abundance, i.e., the proportion of feature j reads in sample i, ZIBSeq simply normalizes the feature abundance by dividing read counts of each given feature by the total mapped read counts in the sample:
denote the normalized feature abundance, i.e., the proportion of feature j reads in sample i, ZIBSeq simply normalizes the feature abundance by dividing read counts of each given feature by the total mapped read counts in the sample: 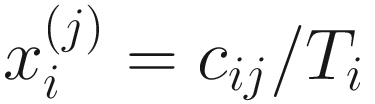 . Thus, the obtained
. Thus, the obtained 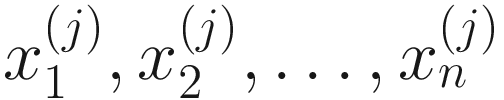 are proportions of feature j, j = 1, …, m on n samples. By assuming that each
are proportions of feature j, j = 1, …, m on n samples. By assuming that each 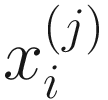 has a probability density function (13.3) with parameters
has a probability density function (13.3) with parameters 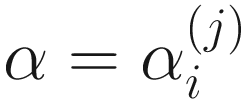 ,
, 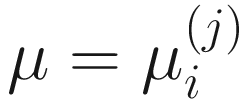 , and
, and 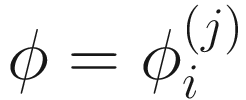 . To fit the parameters in mixture distribution (13.3) for feature j, the ZIBSeq model is defined as below:
. To fit the parameters in mixture distribution (13.3) for feature j, the ZIBSeq model is defined as below: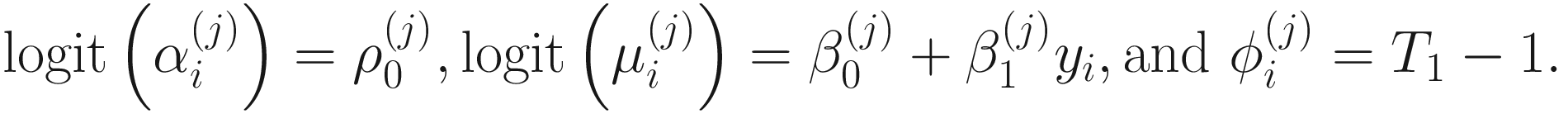
In the above equations, 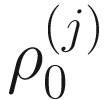 ,
, 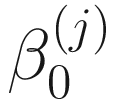 , and
, and 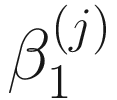 are unknown regression parameters to be estimated, while yi is an outcome measurement indicating the class of sample i, while Ti is the ith sample depth. The dispersion parameter ϕ in (13.4) is approximated by a binomial distribution and a beta distribution under parameterization in (13.1). First, assume the number of reads on a particular feature c follows a binomial distribution with the sample depth T and the probability that the sample reads in this feature μ. Second, let
are unknown regression parameters to be estimated, while yi is an outcome measurement indicating the class of sample i, while Ti is the ith sample depth. The dispersion parameter ϕ in (13.4) is approximated by a binomial distribution and a beta distribution under parameterization in (13.1). First, assume the number of reads on a particular feature c follows a binomial distribution with the sample depth T and the probability that the sample reads in this feature μ. Second, let 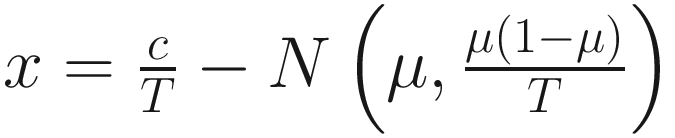 , then, the variance of proportion x will be
, then, the variance of proportion x will be 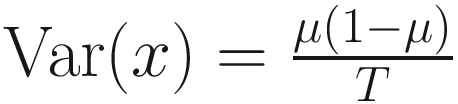 . Third, in the case, the proportion x follows a beta distribution under parameterization in (13.1), the variance will be
. Third, in the case, the proportion x follows a beta distribution under parameterization in (13.1), the variance will be 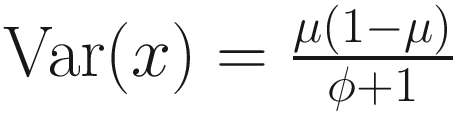 . An approximation of the dispersion parameter ϕ: ϕ ≈ T − 1 is derived from these two forms of variance.
. An approximation of the dispersion parameter ϕ: ϕ ≈ T − 1 is derived from these two forms of variance.
13.2.1.2 Statistical Hypothesis Testing of Microbiome Composition and Outcome
The statistical hypothesis testing of no significant difference in relative abundance of taxa between class membership or experimental conditions is given as: 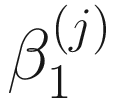 = 0. For large samples, the true null distributions can be approximated by a chi-squared distribution. ZIBSeq takes numerical approach to conduct the statistical hypothesis testing of null distributions to find the maximum likelihood estimates in (13.4). The t-statistic and corresponding P-value are obtained by implementing R package GAMLSS (Stasinopoulos and Rigby 2007).
= 0. For large samples, the true null distributions can be approximated by a chi-squared distribution. ZIBSeq takes numerical approach to conduct the statistical hypothesis testing of null distributions to find the maximum likelihood estimates in (13.4). The t-statistic and corresponding P-value are obtained by implementing R package GAMLSS (Stasinopoulos and Rigby 2007).
13.2.2 Implement ZIBseq
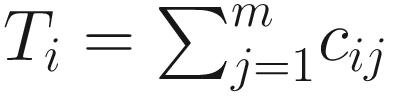 denotes the total number of reads of sample i. Each count cij not only depends on the reads of taxon j but also varies from the sequencing depth: the total number of reads of sample i. In Table 13.1, yi, i = 1, …, n denotes the outcome variable associated with sample i, and it could be class membership of the sample.
denotes the total number of reads of sample i. Each count cij not only depends on the reads of taxon j but also varies from the sequencing depth: the total number of reads of sample i. In Table 13.1, yi, i = 1, …, n denotes the outcome variable associated with sample i, and it could be class membership of the sample.Microbiome data structure for ZIBseq model
Feature1 | Feature2 | … | Featurem | Total | Outcome | |
|---|---|---|---|---|---|---|
Sample1 | c11 | c12 | … | c1m | T1 | y1 |
Sample2 | c21 | c22 | … | c2m | T2 | y2 |
… | … | … | … | … | ||
Samplen | cn1 | cn2 | … | cnm | Tn | yn |
data is a matrix recording count data, which could be extracted from a data frame with samples (or cases) as rows and taxa (or variables) as columns format recording the sample (or meta) and count data.
outcome is a categorical vector of a clinical condition or treatment.
transform is logical value indicating the square-root transform of the compositional matrix.
alpha is used for customized threshold for calculating Q-values.
After running this function, the significant feature (“sigFeature”), the features that have been concerned (“useFeature”), and both Q-value (“qvalue”) and P-value (“pvalue”) will be provided in the output.
Data is from our study (2015) “Lack of Vitamin D Receptor Causes Dysbiosis and Changes the Functions of the Murine Intestinal Microbiome” (Jin et al. 2015). This dataset has been used in our previous book Statistical Analysis of Microbiome Data with R (Xia et al. 2018b).
The “otu_table_fecal_genus_vdr.csv” is a csv file containing 16S rRNA sequencing data matrix for the study samples. The VDR mice abundance data provides the absolute sequence read counts for a total of 240 taxa at the genus rank level (rows) in 8 samples (columns), preprocessed as described in the main article. Among these eight samples, five samples with VDR were knockout and the remaining three samples were wild types. We are interested in whether dysbiosis and functions of intestinal microbiome are associated with the VDR knockout. Thus, the main metadata is the VDR condition status. We can provide additional metadata, which could be a CSV file containing the sample metadata in the data matrix to run the ZIBSeq. Here, we use commands to extract the grouping information from the sequencing data matrix.
Step 1: Load the dataset.
Step 2: Create grouping variable.
Step 3: Merge grouping and abundance taxa datasets to create a data frame.
The data frame has 249 columns, the first column is grouping variable, the remaining 248 columns are taxa.
Of course, we can create a meta dataset a priori and then load it into R and merge it to taxa abundance dataset.
Then, we can perform ZIBSeq analysis. The following steps including screening features, normalizing and transforming data as well as correcting multiple hypothesis testing are processed automatically by the ZIBSeq() function or through specifying such as to specify transform = TRUE or T will do a square root or cube root transformation. We explicitly list them below for reminding us what are really the function ZIBSeq() working on.
Step 4: Filter low abundant features.
Because taxa with a small number of reads are not reliable, so the function first remove any features with total counts less than 2 time large of the sample size to reduce the effects of noises and measurement errors.
Step 5: Normalize and transform data.
ZIBSeq uses a simple normalization procedure to convert the raw abundance measure to a proportion by dividing each feature read count by the total feature read counts in the sample, which results in relative abundance measure ranging [0,1). After normalization, a square root or cube root transformations is performed to ensure the proportion data are better fitting a beta distribution if the distributions of the proportion are extremely left skewed.
Step 6: Define testing features, construct design matrix and run ZIBseq.
Step 7: Correct multiple hypothesis testing.
Step 8: Write the results of P-values and Q-values as tables (Table 13.2).
P-values and Q-values from ZIBSeq model
pvalues | qvalues | |
|---|---|---|
1 | 0.144664728056042 | 0.125896940419006 |
2 | 0.198205269193142 | 0.139233854649929 |
3 | 0.00566793498498382 | 0.0358341428141313 |
4 | 0.142450703458304 | 0.125896940419006 |
5 | 0.650347961806409 | 0.249191944808199 |
6 | 0.332088919006491 | 0.18256970103783 |
7 | 0.110812381135047 | 0.125896940419006 |
8 | 0.018429552251035 | 0.0776775797080376 |
9 | 0.491903363519228 | 0.230365895238663 |
10 | 0.149481602689104 | 0.125896940419006 |
11 | 0.108146886935789 | 0.125896940419006 |
12 | 0.0748980599117641 | 0.125896940419006 |
13 | 0.447131785785204 | 0.217452473513295 |
14 | 0.0272155845567047 | 0.0860319628188012 |
15 | 0.606042815146284 | 0.242436357692026 |
16 | 0.107965948361024 | 0.125896940419006 |
17 | 0.0580814636233615 | 0.125896940419006 |
18 | 0.16028183039337 | 0.125896940419006 |
19 | 0.940513377708146 | 0.312956183240814 |
20 | 0.598904276700515 | 0.242436357692026 |
21 | 0.248405777366409 | 0.149570020619097 |
22 | 0.319334489842356 | 0.18256970103783 |
23 | 0.583495023804528 | 0.242436357692026 |
24 | 1.4105582565407e-05 | 0.000178358242098557 |
25 | 0.719627307693503 | 0.26658254635945 |
26 | 0.0729887026803861 | 0.125896940419006 |
27 | 0.785921203458262 | 0.27604422186671 |
28 | 0.242279775107805 | 0.149570020619097 |
29 | 0.737900153014585 | 0.26658254635945 |
30 | 0.133376612225457 | 0.125896940419006 |
31 | 0.169262963895601 | 0.125896940419006 |
32 | 0.388342311067966 | 0.196415998030281 |
33 | 0.920725205848764 | 0.312956183240814 |
34 | 0.3590536291346 | 0.189169116242343 |
35 | 0.240428856352592 | 0.149570020619097 |
36 | 0.530026294775602 | 0.239354468760951 |
37 | 0.085457319818132 | 0.125896940419006 |
38 | 0.613543801741082 | 0.242436357692026 |
13.2.3 Remarks on ZIBSeq
First, ZIBSeq has better performance in terms of large AUC values in identifying differential features based on ROC analysis via the R package ROCR (Sing et al. 2009) as well as can identify biologically important taxa in a real microbiome data application.
Second, ZIBSeq outperformed ZIG model based on two arguments: (1) compared to ZIG, ZIBSeq was more effective on the simulated multinomial distribution (MN) and binomial distribution (BI) data, although ZIG method performed slightly better than ZIBSeq with larger AUC values at different sample sizes with simulated data of zero-inflated Poisson (ZIP) and zero-inflated negative binomial (ZINB) distributions. (2) ZIBSeq method is more stable, whereas ZIG method is more likely to obtain negative Q-values because it tends to produce more small P-values. Thus, ZIG method may violate the assumption of uniform distribution in the Q-value calculation algorithm proposed by Storey and Tibshirani (2003).
Third, it almost had the same performance whether the response variable (features) is transformed with square root or not transformed in ZIBSeq.
ZIBSeq directly models the proportion after using the Total Sum Scaling (TSS) normalization; in contrast, ZIG models the zero-inflated count data by using the Cumulative Sum Scaling (CSS) normalization (see Sect. 12.1 of Chap. 12); thus, given different approaches of modeling and normalizations used in ZIBSeq and ZIG methods, it is no surprise that ZIBSeq method had better performance for simulated MN, and BI data, while ZIG method had better performance with simulated ZIP and ZINB data.
This kind of approach was criticized as being not able to incorporate the inter-taxa correlation (Li et al. 2018; Liu and Lin 2018) and cannot provide P-values and correct statistical inferences for the selected taxa (Liu and Lin 2018).
This kind of two-part beta regression model was also criticized that cannot provide a straightforward interpretation of covariate effects on the overall marginal (unconditional) mean (Chai et al. 2018).
Cross-sectional two-part beta regression models including ZIBSeq method can handle zero-inflated proportion data; they cannot deal with repeatedly measured proportion data or longitudinal data (Chen and Li 2016).
ZIBSeq uses GAMLSS package to conduct statistical hypothesis testing the significance, which generates t-statistic and corresponding P-value. Currently the tests are limited for two classes of samples or conditions. For more than two classes, multiple binary recoding is needed before apply zero-inflated beta regression to the recoded outcomes.
13.3 Zero-Inflated Beta-Binomial Model (ZIBB)
ZIBB is another specifically developed model for microbiome data based on zero-inflated beta regression.
13.3.1 Introduction to ZIBB
ZIBB (Hu et al. 2018) was proposed based on zero-inflated beta-binomial model to detect the association of microbiome with a continuous or categorical phenotype of interest. ZIBB model assumes that the count data distribution consists of a mixture of a point mass probability at zero (zero model) and a beta-binomial distribution (count model). Thus, ZIBB model has two components: (1) a zero model accounting for excess zeros and (2) a count model (the remaining component) allowing for over-dispersion effects through beta-binomial regression, which may have an appreciable additional mass at zero. The proposed ZIBB method is an extension of the beta-binomial model of BBSeq (Zhou et al. 2011) that was developed for the analysis of RNA sequence count data. Employing zero-inflated modeling and considering a constrained approach to estimate the over-dispersion parameters have been considered as two major improvements in the proposed ZIBB framework (Hu et al. 2018).
13.3.1.1 Zero and Count Models in ZIBB
ZIBB was proposed for analysis of 16S rRNA sequence count data, a m × n sequence count matrix with columns representing samples and rows representing OTUs (ASVs/Taxa). Let Y = (yij) ∈ Ζm × n be the count matrix, and each element yij represents the count of OTU i in sample j, where (i = 1, …, m, j = 1, …n). Let 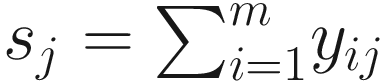 be the library size for sample j. Then, the distribution of microbiome counts data is modeled by a two-stage canonical beta-binomial model, which assuming yij follows a binomial distribution Bin(sj, μij), and μij~Beta(α1ij, α2ij). The probability mass function of the beta-binomial distribution with parameter (sj, α1ij, α2ij) is written as f(⋅| α1ij, α2ij) or
be the library size for sample j. Then, the distribution of microbiome counts data is modeled by a two-stage canonical beta-binomial model, which assuming yij follows a binomial distribution Bin(sj, μij), and μij~Beta(α1ij, α2ij). The probability mass function of the beta-binomial distribution with parameter (sj, α1ij, α2ij) is written as f(⋅| α1ij, α2ij) or
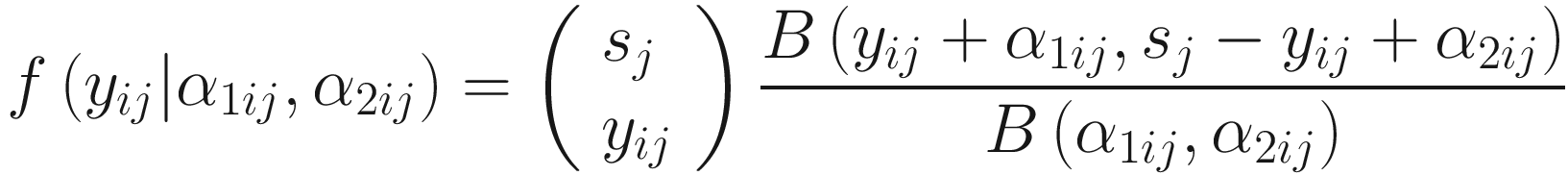
E(μij) = α1ij/(α1ij, α2ij) and ϕiE(μij)(1 − E(μij)). And it is trivial to solve that α1ij = E(μij)(1 − ϕi)/ϕi and α2ij = (1 − E(μij))(1 − ϕi)/ϕi.
Through reparameterizing the parameters (α1ij, α2ij) of the beta distribution to (E(μij), ϕi), ϕi ≥ 0 in the reparameterized form can be clearly interpreted as the over-dispersion parameter. ZIBB model is a mixture of a point mass at zero (zero model) and a beta-binomial distribution (count model). The density of count yij is written as:
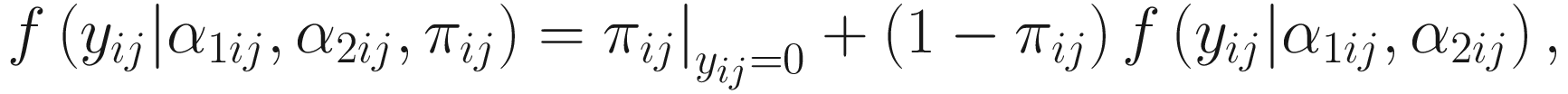
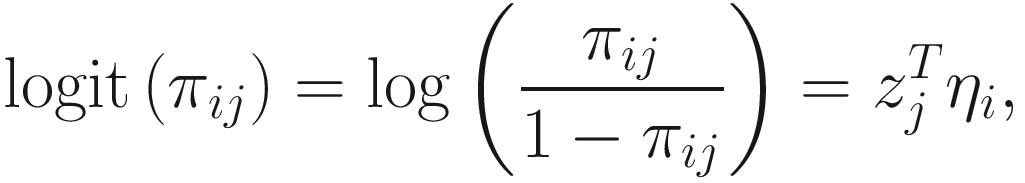
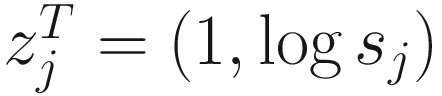 . The link function of the count model is given below:
. The link function of the count model is given below: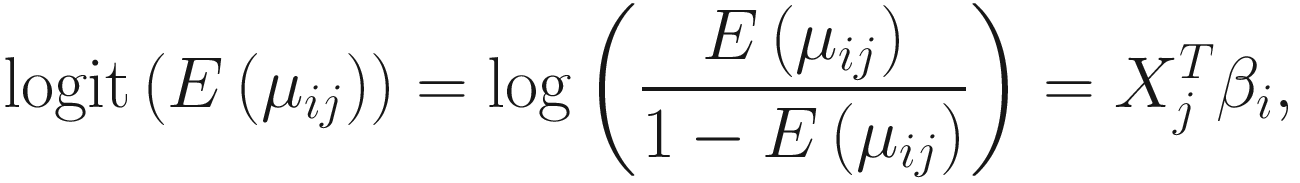
To model the relationship between the mean and the variance, as well as between the mean and the over-dispersion. ZIBB uses the polynomial fit:
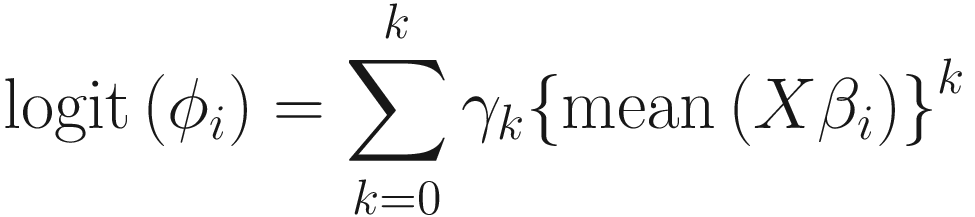
The strategy of considering a constrained approach to model the over-dispersion as a polynomial function of the systematic (mean) component of the generalized linear model was adopted from BBSeq (Zhou et al. 2011). Based on the authors of ZIBB, K = 3 is typically sufficient to effectively model the relationship.
The distinctive feature of ZIBB lies on its modeling the mean-over-dispersion relationship. Thus, the authors of ZIBB called their model and the associated estimation approach as the constrained model and name the model that estimates ϕi separately for each OTU i as the free model.
13.3.1.2 Statistical Hypothesis Testing in ZIBB
ZIBB conducts parameter estimation by two steps: First, estimates the parameters in the free model by the maximum likelihood, and then uses the estimates of parameters in the constrained model to fit the polynomial model according to (13.9) and uses least squares solutions to estimate the parameters in γk’s. The main purpose of ZIBB is to test associations of OTUs with an experimental phenotypes of interest. Thus, statistical hypothesis testing is to test the statistical significance of β1i for each OTU i, i = 1, …, m. The null hypothesis is given as: H0 : β1i = 0. With P = 2, βi = (β0i, β1i)T.
The Wald testing statistic is 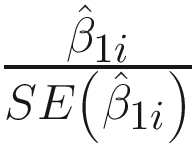 . For discrete (e.g., group indicator) phenotype of microbiome count data sets, a t distribution with degrees of freedom n − 2 is used to approximate the distribution of the Wald statistic under the null hypothesis, while for a continuous (e.g., body mass index values) of phenotype, a standard normal is used to approximate the Wald statistic’s null distribution.
. For discrete (e.g., group indicator) phenotype of microbiome count data sets, a t distribution with degrees of freedom n − 2 is used to approximate the distribution of the Wald statistic under the null hypothesis, while for a continuous (e.g., body mass index values) of phenotype, a standard normal is used to approximate the Wald statistic’s null distribution.
13.3.2 Implement ZIBB
ZIBB for the discovery analysis is implemented via the R package ZIBBSeqDiscovery. ZIBBSeqDiscovery uses zero-inflated beta-binomial model to analyze microbiome count data to detect the associate between phenotype of interest and the composition of the counts. The interested covariates can be adjusted via the link functions of zero and count models. The moment corrected correlation (MCC) approach is applied to adjust the P-values.
ZIBBSeqDiscovery takes two approaches to fit the ZIBB model: (1) The free approach treats the over-dispersion parameters for OTUs as independent, and (2) the constrained approach uses a mean-over-dispersion relationship to the count data.
dataMatrix is the count matrix (m by n, m is the number of OTUs and n is the number of samples).
X is the design matrix (n by p, p is the number of covariates) for the count model (e.g., beta-binomial), and intercept is included. The second column is assumed to be the covariate of interest.
ziMatrix is the design matrix (n by q, q is the number of covariates) for the zero model, and intercept is included.
mode is used to specify either “free” or “constrained” approach is used to estimate over-dispersion parameters.
gn is used to specify a polynomial with degree of freedom gn to fit the mean-over-dispersion relationship. The default value for gn is 3. It is only used in constrained approach, thus gn is only valid when mode = “constrained”.
betastart is used for specifying the initial values for beta estimation matrix (p by m). Where beta are the effects (or coefficients) for the count model.
psi.start is used to specify the initial values for the logit of over-dispersion parameters vector (with length m).
eta.start is used to specify the initial values for eta estimation matrix (q by m), where eta are the effects (or coefficients) for the zero model.
The arguments psi. betastart, psi.start, and eta.start are required only in constrained approach; they should be assigned as the beta estimation matrix, the psi estimation vector, and the eta estimation matrix, respectively, from free approach.
In the ZIBBSeqDiscovery package, the covariate of interest is referred to as phenotype. Current version (latest version 1.0, March 2018) of this package only considers one phenotype. In the design matrix X, the first column is the intercept, and the phenotype of interest is assumed to corresponding to the second column.
betahat for the estimation matrix of beta (p by m) for count model.
bvar for the estimation matrix of the variance of estimated betahat (p by m).
p for the vector (with length of m) of P-values corresponding to the phenotype, in which the ith P-value corresponds to the hypothesis test of H0 : β1i = 0for OTU i.
psi for the estimation vector of the logit of the over-dispersion parameters (with length m).
zeroCoef for the estimation matrix of eta (q by m) for zero model.
gamma for the estimation vector of the coefficients in the mean-over-dispersion relationship in constrained approach (with length gn+1), which is only available when mode = “constrained” is specified.
Dataset is from Kostic et al. (2012) “Genomic analysis identifies association of Fusobacterium with colorectal carcinoma” (Kostic et al. 2012). Sample collection and preparation, amplification, and processing of 16S sequence data were described as in the main article. The data matrix “otu_table_kostic.csv” is a csv file containing 16S rRNA sequencing data which has 2505 OTUs and 185 samples (90 tumor vs. 95 normal colon microbiota). The metadata matrix “meta_table_kostic.csv” is a csv file containing the health status for the samples in otu-table. The interested phenotype here is the health status for samples.
Since the authors of ZIBB (Hu et al. 2018) showed that constrained modeling of ZIBB is better than its free modeling of ZIBB in terms of the type I errors and power, thus we here only report the constrained version of ZIBB using this dataset.
Step 1: Load datasets.
Step 2: Filter out OTUs and remove those OTUs that have zero count and few non-zero counts across all samples.
The ZIBB methods may fail to converge for a small proportion of OTUs. This typically occurs when OTUs have few (e.g., four or fewer) non-zero counts and for such OTUs. In such case, the power to detect association with experimental variables is small; thus before modeling using ZIBB methods, those OTUs need to be filtered out. For the remaining small number of OTUs that fail to converge (usually 2% or fewer), the ZIBB methods substitute P-values from the MCC package.
In below analysis, we removed all OTUs with zero counts across all samples. Based on the practice, for the discrete case, OTUs with zero counts across any one of groups were also removed.
Step 3: Construct the design matrix and zero inflation related matrix.
We use below commands to construct the design matrix and zero inflation related matrix.
Step 4: Fit the ZIBB model with free approach.
Step 5: Fit the ZIBB model with constrained approach.
Step 6: Use MCC method to adjust the P-values.
NA mostly appears when the OTU counts are zero in most of the samples. In this case, there are 185 samples, thus we want to check the cases such that OTU has 180, 181, 182, 183, and 184 zero counts across the 185 samples, respectively. The following commands can be used to check the effects of MCC adjustment. The NA counts in the reported P-values before and after MCC adjustment will be printed out.
Step 7: Write out the corrected P-values adjusted by the MCC method.
13.3.3 Remarks on ZIBB
Overall, this study (Hu et al. 2018) showed that both zero inflation and the proposed constraint approaches are vital for accurate and powerful analysis of microbiome count data and ZIBB modeling with the constrained approach is preferred among the competing methods, including BBSeq, edgeR, and ZINB. Especially, it was demonstrated (Hu et al. 2018) that in terms of Type I errors and power for both discrete and continuous cases: (1) ZIBB has higher or comparable performance compared to competing methods. (2) Both the approaches of free and the constrained ZIBB modeling can provide accurate standard error estimates. And (3) the constrained modeling of ZIBB outperformed free modeling of ZIBB. However, the ZIBB methods may fail to converge for a small proportion of OTUs. This converge problem typically occurs when OTUs have four or fewer non-zero counts (Hu et al. 2018).
13.4 Summary
In this chapter we first briefly introduced zero-inflated beta modeling microbiome data and then focused on covering two specifically designed two-part zero-inflated beta regression models for microbiome data: ZIBSeq and ZIBB. We introduced their methodological developments and illustrated their applications with real study data. We also commented on their advantages and limitations. In Chap. 14, we will introduce compositional analysis of microbiome data.